How can we define Intrinsic Motivation?

Pierre-Yves Oudeyer,     Frederic Kaplan

Link to the paper
Link to the page of the main author

I hereby again recall that this work is not mine, but the one of:
Pierre-Yves Oudeyer and Frederic Kaplan
I simply try to make a complete summary, that is easier to quickly read than the original paper. Thanks for the authors for contributing to science in such an incredible manner!

 Abstract :

Intrinsic Motivation (IM) is a crucial mechanism for open-ended cognitive development since it is the driver of spontaneous exploration and curiosity.
This paper presents an unified definition of intrinsic motivation, based on the theory of Daniel Berlyne.

Based on this definition, we propose a landscape of types of computational approaches

This concept comes from psychology. It is the mechanism that explains the spontaneous exploratory behaviors observed in humans, and infants in particular.

Intrinsic motivation: doing of an activity for its inherent pleasure rather than the potential reward it could lead to.
Internal motivations involve reward that are produced within the organism.
-> The intrinsic/extrinsic distinction, on the contrary, is not a distinction based on the location of origin of the reward, but on the kind of reward

Example of a child doing his homework:

Drives to manipulate, drives to explore

 Theory of drives (Hull, 1943): According to the theory, the reduction of drives (like hunger or pain) is the primary force behind motivation. One drive to manipulate, and another one to explore.
(One of the biggest problems with Hull’s drive reduction theory is that it does not account for how secondary reinforcers reduce drives. Unlike primary drives such as hunger and thirst, secondary reinforcers do nothing to directly reduce physiological and biological needs. Take money, for example. While money does allow you to purchase primary reinforcers, it does nothing in and of itself to reduce drives. Despite this, money still acts as a powerful source of reinforcement.)

Reduction of cognitive dissonance

Organisms are motivated to reduce dissonance, which is the incompatibility between internal cognitive structures and the situations currently perceived.
However, these theories were criticized on the basis that some human behaviors are also intended to increase uncertainty, and not only to reduce it.

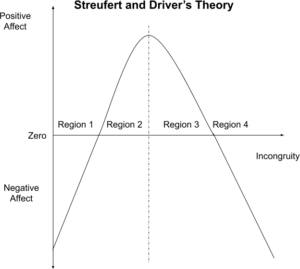
Optimal incongruity

Hunt developed the idea that people look for optimal incongruity.
Interesting stimuli were those where there was a discrepancy between the perceived and standard levels of the stimuli.
Berlyne developed similar notions as he observed that the most rewarding situations were those with an intermediate level of novelty

Motivation for effectance, personal causation, competence and self-determination

The concept of challenge replace the notion of optimal incongruity.
Basically, these approaches argue that what motivates people is the degree of control they can have on other people, external objects and themselves, or in other words, the amount of effective interaction. (Theory of “Flow” (Csikszentmihalyi, 1991))

Diverse theoretical approaches proposed, no consensus.
The view of Daniel Berlyne (Berlyne, 1965) shall be used as a fruitful theoretical reference for developmental roboticist.

The central concept is collative variables:
The probability and direction of specific exploratory responses can apparently be influenced by many properties of external stimulation, as well as by many intraorganism variables. They can, no doubt, be influenced by stimulus intensity, color, pitch, and association with biological gratification and punishment, … [but] the paramount determinants of specific exploration are, however, a group of stimulus properties to which we commonly refer by such words as “novelty”, “change”, “surprisingness”, “incongruity”, “complexity”, “ambiguity”, and “indistinctiveness”.
These properties possess close links with the concepts of information theory, and can all be discussed in information-theoretic terminology

Ambiguity, indistinctiveness: undoubtebly due to a gap in available information

Novelty, complexity: uncertainty about pattern organisation, labelling, on what will be perceived next

Surprisingness, incongruity: discrepancy between information embodied in expectations and perceived information
the term “collative” is proposed to denote all these stimulus properties collectively, since they all depend on comparison of information from different stimulus elements
-> here we speak of subjective uncertainty

There are “intrinsic” forms of motivation which collaborate with extrinsic motivation in regulating exploratory or epistemic activity but are also capable of actuating exploratory or epistemic activity on their own. Intrinsic motivation depends primarily on the collative properties of the external environment.

An activity is intrinsically motivating for an autonomous entity if its interest depends primarily on the collation or comparison of information from different stimuli. 

🚨 The information that is compared has to be understood in an information theoretic perspective, in which what is considered is the intrinsic mathematical structure of the values of stimuli, independently of their meaning.

Berlyne’s theory is used as a common conceptual framework to interprete and compare the various computational architectures. It excludes a number of internal motivation mechanisms from intrinsic motivation mechanisms, but has many mechanisms that have not been explored yet in the computational literature. 

Notation: 

• e^k : event/situation/activity
• E: whole space of possible events (not predefined but discoverable by the robot)
• t : time step
• r(e^k, t) = measure of interestingness of e^k at t. (reward)
• si: a sensory chanel of the robot (low or high level)
• mi: a motor chanel of the robot
• SM(t): vector of all sensorimotor values at time t is denoted 

Space of computational models of intrinsic motivation is here organized into three broad classes that all share the same formal notion of a sensorimotor flow experienced by a robot:

1. Knowledge based models: comparisons between the predicted flow of sensorimotor values, based on an internal forward model, with the actual flow of values
   -> adaptive motivation (to mechanisms that assign different levels of interest to the same situation/activity depending on the particular moment in development where it is encountered)
2. Competence based models: comparisons between self-generated goals, which are particular configurations in the sensorimotor space, and the extent to which they are reached in practice, based on an internal inverse model that may be learned
   -> adaptive motivation
3. Morphological models:  measures of the immediate structural relationships among multiple sensorimotor channels (which are not based on long-term knowledge or competence previously acquired by the agent)
   -> fixed motivations

The principle is to measures the dissonances between:

• the situations experienced 
• the knowledge and expectations that the robot has.

There are two sub-approaches related to the way knowledge and expectations are represented: information theoretic/distributional and predictive.
From now on, we’ll make use of e^k instead of SM^k to describe the states.

The robot uses representations that estimate the distributions of probabilities of observing certain events ek in particular contexts.

Uses the probability of 

• observing a certain state in the sensorimotor flow P(e^k)
• observing particular transitions between states P(e^k(t), e^l(t))
• observing a particular state after a given state P(e^k(t+1) | e^l(t))

e^k can either be direct numerical prototypes or complete regions within the sensorimotor space

We’ll use the concept of entropy (for discretized space):
H(E)=-\sum_{e^{k} \in E} P\left(e^{k}\right) \ln \left(P\left(e^{k}\right)\right) which correspond to the average quantity of information that the observation of an event bring to the robot.

Uncertainty motivation (UM) corresponds to the tendency to be intrinsically attracted by novelty.
Implementation: building a system that, for every event e^{k} that is actually observed, will generate a reward r(e^{k}) inversely proportional to its probability (so far) of observation:
r\left(e^{k}, t\right)=C \cdot\left(1-P\left(e^{k}, t\right)\right), where C is a constant

Information gain motivation (IGM) corresponds to the “pleasure of learning”.

Implementation: decrease of uncertainty in the knowledge that the robot has of the world after an event e^{k} has happened:
r\left(e^{k}, t\right)=C \cdot(H(E, t)-H(E, t+1)).
In practice, it is not necessarily tractable in continuous space, which is potentially a common problem to all distributional approaches.

Empowerment (EM) is a reward measure that pushes an agent to produce sequences of actions that can transfer a maximal amount of information to its sensors through the environment. The agent is thus motivated to do actions that matters, i.e., that have a big impact on the environment.

Implementation: It is defined as the channel capacity from the sequence of actions A_t, A_{t+1}, ..., A_{t+n-1} to the perceptions S_{t+n} after an arbitrary number of timesteps:
r\left(A_{t}, A_{t+1}, \ldots, A_{t+n-1} \rightarrow S_{t+n}\right)=\max _{p(\vec{a})} I\left(A_{t}, A_{t+1}, \ldots, A_{t+n-1}, S_{t+n}\right)

where p(\vec{a}) is the probability distribution function of the action sequences \vec{a}=\left(a_{t}, a_{t+1}, \ldots, a_{t+n-1}\right) and I is mutual information.

For me empowerment sounds more like a competence based approach rather than a information based one, here empowerement is about maximizing the information perceived, which can help the agent make wiser decision, so I like to personnally use another term, such as Omniscience.

“Often, knowledge and expectations in robots are not represented by complete probability distributions, but rather based on the use of predictors such as neural networks or support vector machines that make direct predictions about future events.”

Some more notation:
\Pi: Predictor (neural network or other model)
S M(\rightarrow t): current sensorimotor context (and possibly the past contexts)
\Pi(S M(\rightarrow t))=\widetilde{e}^{k}(t+1): prediction of the system
E_{r}(t)=\left\|\tilde{e}^{k}(t+1)-e^{k}(t+1)\right\|error of prediction.

Predictive novelty motivation (NM) also tries to enhance novelty. Thus, interesting situations are those for which the prediction errors are highest.
Implementation:
r(S M(\rightarrow t))=C \cdot E_{r}(t)

Intermediate level of novelty motivation (ILNM) follows the idea that humans are attracted by situations of intermediate/optimal incongruity. A too predictive situation might be boring while a completely nonsense one might provide anxiety.

Implementation: We thus introduce a threshold E_{r}^{\sigma}
r(S M(\rightarrow t))=C_{1} \cdot e^{-C_{2} \cdot\left\|E_{r}(t)-E_{r}^{\sigma}\right\|^{2}}

Learning progress motivation (LPM) to avoid the problem of setting a threshold. It models intrinsic motivation with a system that generates rewards when predictions improve over time. Thus, the system will try to maximize prediction progress(or decrease of PE). It corresponds here to knowledge acquisition instead of pure knowledge.

To get a formal model, one needs to be precise and subtle in how the decrease is computed, as this may for example attribute a high reward to the transition between a situation in which a robot is trying to predict the movement of a leaf in the wind (very unpredictable) or a situation in which it just stares at a white wall trying to predict whether its color will change (very predictable).

There are several ways to implement LPM:

1. Here the predictor will be updated after observing the event (be slightly modified to be more able to predict e^k). Thus we can define a prediction error, from the predictor, before the update (E_r(t)), and a prediction error after the update, with an updated agent , and its corresponding error:
   E_{r}^{\prime}(t)=\left\|\Pi^{\prime}(S M(\rightarrow t))-e^{k}(t+1)\right\|.
   This allows us to define a “progress” in the prediction error.
   r(S M \rightarrow t)=E_{r}(t)-E_{r}^{\prime}(t)
2. Another approach to compute learning progress is to use a mechanism that will allow the robot to group similar situations into regions \mathcal{R}_{n} within which the comparison is meaningful. The number and boundaries of these regions are typically adaptively updated. Then, for each of these regions, the robot monitors the evolution of prediction errors, and makes a model of their derivative, which defines learning progress, and thus reward, in these regions. If SM(t) belongs to the region \mathcal{R}_{n}, we can define the mean of predictions errors of the predictor in the last \tau predictions made about sensorimotor situation <E^{\mathcal{R}_{n}}(t)>.
   Then the reward is defined by the progression:
   r(S M(\rightarrow t))=<E_{r}^{R_{n}}(t-\theta)>-<E_{r}^{R_{n}}(t)>

Predictive familiarity motivation (FM) refers push organisms to explore their environment. A slight mathematical variation of NM would model a motivation to search for situation which are very predictable, and thus familiar:
r(S M(\rightarrow t))=\frac{C}{E_{r}(t)}

This would be considered intrinsic, despite the fact that it prevents the agents from exploring the environment.

Here we are interested in the competence that an agent has for achieving self-determined results or goals. It relies on psychological concepts of 

• effectance, 
• personal causation
• competence 
• self determination 
• “Flow” 

We here need the concept of challenge with the measure of complexity as well as the measure of performance.
A challenge is here a sensorimotor configuration that the individual sets by itself and try to achieve. (Could be grasping a ball, relying on the tactile and visual sensors for example).
We can thus define the set \{P_k\} corresponding to a set of properties of a sensorimotor configuration, and the goal g^k = \{P_k\}.
While prediction mechanisms or probability models, as used in previous sections, can be used in the goal-reaching architecture, they are not mandatory (for example, one can implement systems that try to achieve self-generated goals through Q Learning and never explicitly make predictions of future sensorimotor contexts).

Competence based and knowledge based models can look alike and produce very different behaviors, as the capacity to predict what happens in a situation can be sometimes only loosely coupled to the capacity to modify a situation in order to achieve a given self-determined goal (example of the tree leaves).

Here we work with a two level actions, and two level decision architecture. The high level determine what goal should be explored, associated with a first time scale, in which we denote the time t_g, and a lower-level of action consisting in choosing what to do in order to reach the goals.

Whenever a goal g^k(t_g) is set, there is a “know-how” module KH(t_g) that is responsible for planning the lower-level actions in order to reach it and that learns through experience.
After a certain amount of time (could be a timeout), we measure the competence of the agent on goal g^k at time t_g:
\left.l_{a}\left(g_{k}, t_{g}\right)=\| \widehat{g_{k}\left(t_{g}\right)}-g_{k}\left(t_{g}\right)\right) \|

The “interestingness”, and thus reward value, of the goal g^k is then derived from this competence measure.
At time g_{t+1}, another goal is chosen to maximize the expected cumulative reward.

Maximizing incompetence motivation (IM) pushes the robot to set challenges/goals for which its performance is lowest. This is a motivation for maximally difficult challenges. This can be implemented as:
r\left(S M(\rightarrow t), g_{k}, t_{g}\right)=C \cdot l_{a}\left(g_{k}, t_{g}\right)

Maximizing competence progress – aka Flow motivation (CPM). Flow refers to the state of pleasure related to activities for which difficulty is optimal: neither too easy nor too difficult.
(As difficulty of a goal can be modeled by the (mean) performance in achieving this goal, a possible manner to model flow would be to introduce two thresholds defining the zone of optimal difficulty. Yet, the use of thresholds can be rather fragile, require hand tuning and possibly complex adaptive mechanism to update these thresholds during the robot’s lifetime)).

Instead of hand-tuning, we could here to use the progress instead of the pure ability.
Thus, a first manner to implement CPM would be:
r\left(S M(\rightarrow t), g_{k}, t_{g}\right)=C \cdot\left(l_{a}\left(g_{k}, t_{g}-\theta\right)-l_{a}\left(g_{k}, t_{g}\right)\right) corresponding to the difference between the current performance for task g^k and the performance corresponding to the last time g^k was tried (at t_g−θ).
Again, one could smooth the variance by using:
r\left(S M(\rightarrow t), g_{k}, t_{g}\right)=C \cdot\left(<l_{a}\left(g_{k}, t_{g}-\theta\right)>-<l_{a}\left(g_{k}, t_{g}\right)>\right)
Using the current mean, compared to a previous one.

Knowledge and competence based models rely upon measures comparing information perceived in the present and information perceived in the past and represented in memory.
Morphological models compare information characterizing several pieces of stimuli perceived at the same time in several parts of the perceptive field (would compare visual and audio inputs).

Synchronicity motivation (SyncM) is based on an information theoretic measure of short term correlation (or reduced information distance) between a number of sensorimotor channels. With such a motivation, situations for which there is a high short term correlation between a maximally large number of sensorimotor channels are very interesting. This can be formalized in the following manner:
Let us consider that the sensorimotor space SM is a set of n information sources {SM_i} and that possible values for these information sources typically correspond to elements belonging to a finite discrete space. At each time t, an element sm_i corresponds to the information source SM_i and the following notation can be used: SM_i(t) = sm_i.
The conditional entropy for two information sources SM_i and SM_j can be calculated as:
H\left(S M_{j} | S M_{i}\right)=-\sum_{s m_{i}} \sum_{s m_{i}} p\left(s m_{i}, s m_{j}\right) \log _{2} p\left(s m_{j} | s m_{i}\right)

H\left(S M_{j} | S M_{i}\right) is traditionally interpreted as the uncertainty associated with SMj if the value of SMi is known. We can measure synchronicity s(SM_j, SM_i) between two information sources in various manners. One of them is Crutchfield’s normalized information distance (which is a metric) between two information sources, defined as (Crutchfield, 1990):
d\left(S M_{j}, S M_{i}\right)=\frac{H\left(S M_{i} | S M_{j}\right)+H\left(S M_{j} | S M_{i}\right)}{H\left(S M_{i}, S M_{j}\right)}

Based on this definition we can define synchronicity as:
s_{1}\left(S M_{j}, S M_{i}\right)=\frac{C}{d\left(S M_{j}, S M_{i}\right)}

We can also assimilate synchronicity to mutual information:

Or measuring the correlation between two time series:

s_{2}\left(S M_{j}, S M_{i}\right)=\frac{\sum_{t}\left(s m_{i}(t)-\left\langle s m_{i}\right\rangle\right) \cdot\left(s m_{j}(t)-\left\langle s m_{j}\right\rangle\right)}{\sqrt{\sum_{t}\left(s m_{i}(t)-\left\langle s m_{i}\right\rangle\right)^{2}} \cdot \sqrt{\sum_{t}\left(s m_{j}(t)-\left\langle s m_{j}\right\rangle\right)^{2}}}.

Stability motivation (StabM):

pushes to act in order to keep the sensorimotor flow close from its average value:
r(S M(\rightarrow t))=C \cdot\left(\sum_{i} \sum_{j} s\left(S M_{j}, S M_{i}\right)\right)